Penerapan pada Masalah Nyata tentang Pertidaksamaan Nilai Mutlak
Pada topik kali ini, kalian akan mempelajari beberapa masalah nyata dalam kehidupan sehari-hari yang merupakan contoh dari pertidaksamaan mutlak. Jadi, mari kita ingat kembali konsep-konsep dasar pertidaksamaan nilai mutlak.
Berikut ini beberapa bentuk dari pertidaksamaan mutlak.
1. |f(x)| < a dan a > 0
Penyelesaian dari bentuk di atas adalah -a < f(x) < a
2. |f(x)| > a dan a > 0
Penyelesaian dari bentuk di atas adalah f(x) < -a atau f(x) > a
3. |f(x)| > |g(x)|
Bentuk di atas dapat diselesaikan dengan cara mengkuadratkan kedua ruas.
Contoh 1 :
Rata-rata kepadatan lalu lintas udara di Bandara Internasional Soekarno Hatta dalam satu hari adalah 19 pesawat per jam (ppj). Selama jam sibuk, kepadatan lalu lintasnya lebih tinggi, sedangkan selama jam longgar kepadatannya lebih rendah. Tentukan jangkauan dari kepadatan lalu lintas pesawat di Bandara Internasional Soekarno Hatta jika kepadatannya tidak pernah lebih dari 10 ppj dari rata-rata!
Penyelesaian :
Misalkan x adalah kepadatan lalu lintas pesawat di Bandara Internasional Soekarno Hatta, maka masalah di atas dapat dimodelkan menjadi |x - 19| ≤ 10
Adapun penyelesaian dari bentuk di atas adalah sebagai berikut :
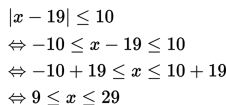
Jadi, jangkauan kepadatan lalu lintas pesawat di di Bandara Internasional Soekarno Hatta lebih dari atau sama dengan 9 ppj dan kurang dari atau sama dengan 29 ppj.
Contoh 2 :
Pengukuran suatu benda dengan jangka sorong dilakukan sebanyak 5 kali dengan data 15 mm ; 14,9 mm, 14,8 mm ; 15,01 mm dan 15 mm. Hitunglah nilai rata-rata data yang sebenarnya jika galat alat pengukuran adalah 0,05 mm!
Penyelesaian :
Misalkan x adalah nilai rata-rata data yang sebenarnya.
Oleh karena pengukuran ini memiliki galat 0,05 mm, maka
Jadi, nilai rata-rata data yang sebenarnya berada pada interval 14,892 ≤ x ≤ 14,992.
Sumber : Quipperschool
