Pada
topik sebelumnya kalian telah mempelajari limit fungsi. Topik kali ini
merupakan kelanjutan dari topik limit fungsi yaitu turunan. Pada topik
ini kalian akan mempelajari definisi dan aturan-aturan pada turunan
fungsi aljabar maupun fungsi trigonometri.
Definisi turunan:
Fungsi
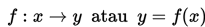mempunyai turunan yang dinotasikan
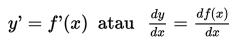dan didefinisikan:
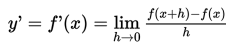atau
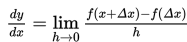
Untuk lebih jelasnya silakan simak contoh-contoh berikut.
Contoh 1:
Tentukan turunan dari f(x) = 4x - 3 .
Jawab:
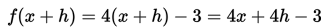Sehingga:
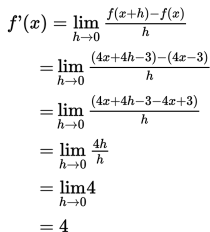
Contoh 2:
Tentukan turunan dari f(x) = 3x2.
Jawab:
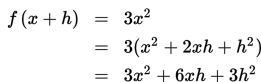Sehingga:
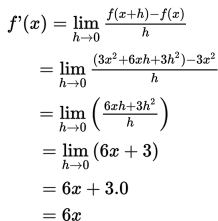
RUMUS-RUMUS TURUNAN
Setelah mempelajari definisi turunan, kalian akan mempelajari rumus-rumus turunan.
Turunan f(x) = axn adalah
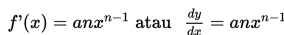
Untuk suatu fungsi u dan v, bilangan real c, dan bilangan rasional n, berlaku :
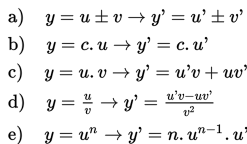
Untuk lebih jelasnya, kalian bisa mencermati contoh berikut.
Contoh 1:
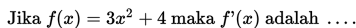
Pembahasan:
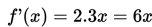
Contoh 2:
Nilai Turunan pertama dari f(x) = 2x3 + 12x2 - 8x + 4 adalah
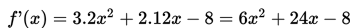
Contoh 3:
Turunan ke- 1 dari
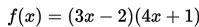adalah ….
Pembahasan:
Contoh 4:
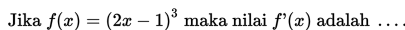
Pembahasan:
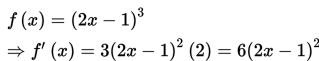
Contoh 5:
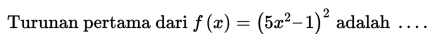
Pembahasan:
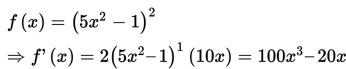
Contoh 6:
Rusuk suatu kubus bertambah panjang dengan laju 7 cm per detik.
Hitunglah laju bertambahnya volume pada saat panjang rusuknya 15 cm.
Pembahasan:
Misal panjang rusuk = x cm
Setelah t detik, panjang rusuk = (x + 7t ) cm maka volume kubus setelah t detik adalah:
Contoh 7:
Suatu perusahaan menghasilkan x produk dengan biaya total sebesar 75 + 2x + 0,1x2 rupiah. Jika semua produk perusahaan tersebut terjual dengan harga Rp 40,00 untuk setiap produknya, maka laba maksimum yang diperoleh adalah ….
Pembahasan:
Biaya untuk x produk sebesar 75 + 2x + 0,1x2 (rupiah)
harga 1 produk = Rp 40,00
Laba maksimal bila L' = 0
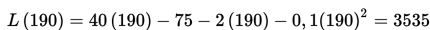
Dengan demikian, laba maksimumnya adalah Rp 3.535,00.
Sumber : Quipper School
Soal Latihan dan Pembahasan
Pembahasan Cara Smart
Video Pembahasan
Definisi turunan:
Fungsi
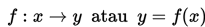
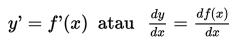
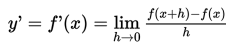
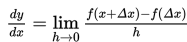
Notasi kedua ini disebut notasi Leibniz.
Untuk lebih jelasnya silakan simak contoh-contoh berikut.
Contoh 1:
Tentukan turunan dari f(x) = 4x - 3 .
Jawab:
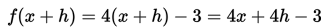
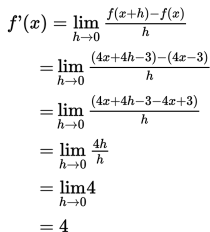
Contoh 2:
Tentukan turunan dari f(x) = 3x2.
Jawab:
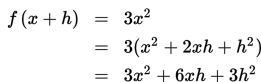
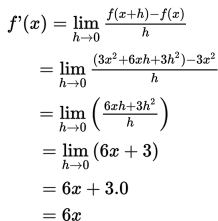
RUMUS-RUMUS TURUNAN
Setelah mempelajari definisi turunan, kalian akan mempelajari rumus-rumus turunan.
Turunan f(x) = axn adalah
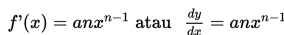
Untuk suatu fungsi u dan v, bilangan real c, dan bilangan rasional n, berlaku :
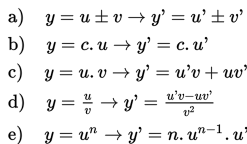
Untuk lebih jelasnya, kalian bisa mencermati contoh berikut.
Contoh 1:
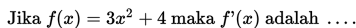
Pembahasan:
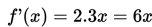
Contoh 2:
Nilai Turunan pertama dari f(x) = 2x3 + 12x2 - 8x + 4 adalah
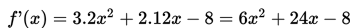
Contoh 3:
Turunan ke- 1 dari
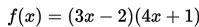
Pembahasan:
Contoh 4:
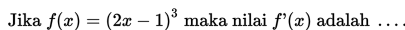
Pembahasan:
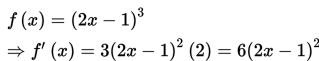
Contoh 5:
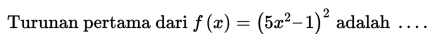
Pembahasan:
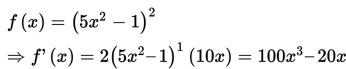
Contoh 6:
Rusuk suatu kubus bertambah panjang dengan laju 7 cm per detik.
Hitunglah laju bertambahnya volume pada saat panjang rusuknya 15 cm.
Pembahasan:
Misal panjang rusuk = x cm
Setelah t detik, panjang rusuk = (x + 7t ) cm maka volume kubus setelah t detik adalah:
Contoh 7:
Suatu perusahaan menghasilkan x produk dengan biaya total sebesar 75 + 2x + 0,1x2 rupiah. Jika semua produk perusahaan tersebut terjual dengan harga Rp 40,00 untuk setiap produknya, maka laba maksimum yang diperoleh adalah ….
Pembahasan:
Biaya untuk x produk sebesar 75 + 2x + 0,1x2 (rupiah)
harga 1 produk = Rp 40,00
Laba maksimal bila L' = 0
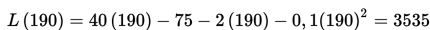
Dengan demikian, laba maksimumnya adalah Rp 3.535,00.
Sumber : Quipper School
Nah, kamu telah selesai belajar tentang Konsep Turunan.
Literasi Unit Kegiatan Belajar Mandiri (UKBM)
(di sini)
Literasi Unit Kegiatan Belajar Mandiri (UKBM)
(di sini)
Agar pemahamanmu bertambah lagi, yuk kerjakan latihan soal-soal berikut ini. Selamat berlatih.
Soal Latihan dan Pembahasan
Pembahasan Cara Smart
Video Pembahasan
