Apakah
kalian pernah mendengar istilah irisan kerucut? Salah satu irisan
kerucut adalah bentuk parabola. Pada sebuah parabola terdapat garis dan
titik yang saling berhubungan yang merupakan unsur-unsur penyusun
parabola tersebut.
Untuk mempelajari istilah-istilah dalam parabola, mari kita perhatikan beberapa contoh grafik fungsi parabola berikut ini.
Bagaimana cara memperoleh persamaan parabola yang puncaknya tidak terletak pada titik (0,0)?
Untuk parabola yang puncaknya di titik (a,b) maka parabola semula berpuncak di titik (0,0) akan mengalami pergeseran sejauh :
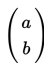sehingga untuk persamaan parabola dengan bentuk x2 = 4py yang semula mempunyai puncak di titik (0,0) sekarang puncaknya terletak di titik (a,b) dan persamaan parabola menjadi (x - a)2 = 4p(y - b)
Selanjutnya, untuk persamaan parabola dengan bentuk y2 = 4px yang berpuncak di (0,0) digeser sejauh :
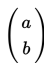maka puncak koordinat puncak menjadi di titik (a,b) dan persamaan parabola menjadi :
(y - b)2 = 4p(x - a)
Mari kita cermati beberapa contoh berikut ini.
Contoh 1
Tentukan persamaan garis direktriks dari parabola y2 = 8x
Penyelesaian
Persamaan parabola y2 = 8x sesuai dengan bentuk umum y2 = 4px dengan titik puncak di (0,0).
Karena 8x = 4px <=> p = 2 maka persamaan garis direktrisnya adalah x = -p <=> x = -2
Contoh 2
Tentukan persamaan parabola jika koordinat titik puncak (0,0), fokus (0,-1), dan sumbu Y adalah sumbu simetri!
Penyelesaian
Oleh karena puncak parabola (0,0) dan titik fokus adalah (0, -1) maka p = 1.
Dengan demikian, persamaan parabola yang dimaksud adalah x2 = 4y
Sumber : Quipper School
Nah, kamu telah selesai belajar tentang Irisan Kerucut - Parabola. Agar pemahamanmu bertambah lagi, yuk kerjakan latihan soal-soal berikut ini. Selamat berlatih.
Soal Latihan dan Pembahasan
Pembahasan Cara Smart
Video Pembahasan
Untuk mempelajari istilah-istilah dalam parabola, mari kita perhatikan beberapa contoh grafik fungsi parabola berikut ini.
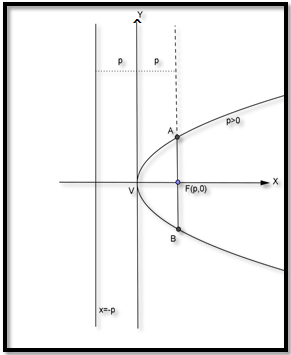
- Persamaan parabola : y2 = 4px
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(p,0) -> Jika p > 0 maka parabola terbuka ke kanan
- Sumbu simetri : sumbu X
- Persamaan garis direktriks : x = -p
- Panjang latus rectum : AB = 4|p|
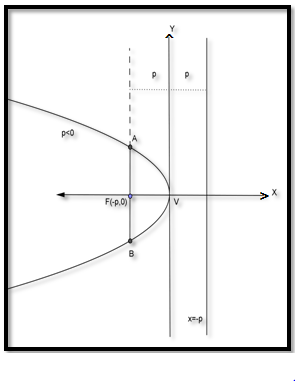
- Persamaan parabola : y2 = 4px
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(-p,0) -> Jika p < 0 maka parabola terbuka ke kiri
- Sumbu simetri : sumbu X
- Persamaan garis direktriks : x = p
- Panjang latus rectum : AB = 4|p|
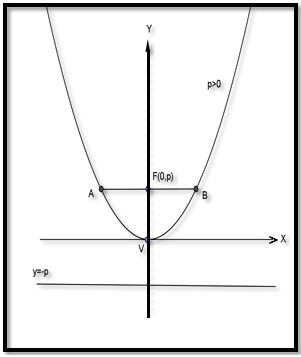
- Persamaan parabola : x2 = 4py
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(0,p) -> Jika p > 0 maka parabola terbuka ke atas
- Sumbu simetri : sumbu Y
- Persamaan garis direktriks : y = -p
- Panjang latus rectum : AB = 4|p|
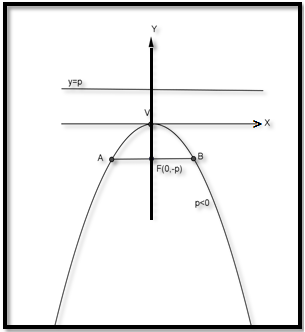
- Persamaan parabola : x2 = 4py
- Koordinat titik puncak : V(0,0)
- Koordinat titik fokus : F(0,-p) -> Jika p < 0 maka parabola terbuka ke atas
- Sumbu simetri : sumbu Y
- Persamaan garis direktriks : y = p
- Panjang latus rectum AB = 4|p|
Bagaimana cara memperoleh persamaan parabola yang puncaknya tidak terletak pada titik (0,0)?
Untuk parabola yang puncaknya di titik (a,b) maka parabola semula berpuncak di titik (0,0) akan mengalami pergeseran sejauh :
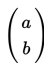
Selanjutnya, untuk persamaan parabola dengan bentuk y2 = 4px yang berpuncak di (0,0) digeser sejauh :
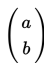
(y - b)2 = 4p(x - a)
Mari kita cermati beberapa contoh berikut ini.
Contoh 1
Tentukan persamaan garis direktriks dari parabola y2 = 8x
Penyelesaian
Persamaan parabola y2 = 8x sesuai dengan bentuk umum y2 = 4px dengan titik puncak di (0,0).
Karena 8x = 4px <=> p = 2 maka persamaan garis direktrisnya adalah x = -p <=> x = -2
Contoh 2
Tentukan persamaan parabola jika koordinat titik puncak (0,0), fokus (0,-1), dan sumbu Y adalah sumbu simetri!
Penyelesaian
Oleh karena puncak parabola (0,0) dan titik fokus adalah (0, -1) maka p = 1.
Dengan demikian, persamaan parabola yang dimaksud adalah x2 = 4y
Sumber : Quipper School
Nah, kamu telah selesai belajar tentang Irisan Kerucut - Parabola. Agar pemahamanmu bertambah lagi, yuk kerjakan latihan soal-soal berikut ini. Selamat berlatih.
Soal Latihan dan Pembahasan
Pembahasan Cara Smart
Video Pembahasan
