Luas Daerah Antara Kurva dan Sumbu x

Coba amati dedaunan di sekitarmu. Tentunya permukaan daun tersebut tidak seperti lingkaran, persegi, belah ketupat, atau bangun datar lainnya. Pernahkah kamu berfikir bagaimana cara menentukan luas permukaan daun tersebut? Untuk menghitung luas daun tersebut, kita dapat menggunakan integral tentu.

Dengan mengasumsikan tepi-tepi daun sebagai sebuah kurva, kita dapat menghitung luas permukaan daun tersebut. Konsep inilah yang akan kita pelajari pada sub-bab ini, yaitu luas daerah antara kurva dan sumbu–

x

. Untuk itu, perhatikanlah materi ini dengan seksama.

Dalam mempelajari luas daerah antara kurva dengan sumbu–

x

, kita akan membahas beberapa kasus, yaitu; kurva yang tidak memotong sumbu–

x

dan kurva yang memotong sumbu-

x

Untuk lebih jelasnya perhatikan kasus-kasus berikut.

Kurva Tidak Memotong Sumbu- $x$

1. Daerah terletak di atas sumbu- $x$

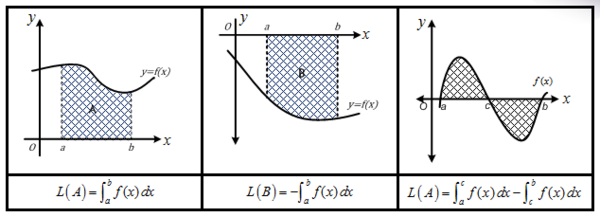
Misalkan

A

adalah daerah yang dibatasi kurva

y = f (x), x = a, x = b

, dan sumbu-

x

, dengan

f (x) \geq 0

(kurva tidak memotong sumbu–

x

). Luas daerah

A

tersebut kita lambangkan dengan

L (A)

dapat dihitung dengan integral berikut.

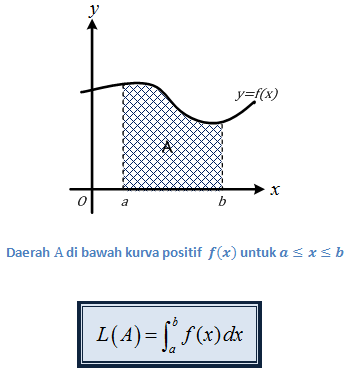
2. Daerah terletak di bawah sumbu- $x$

Cara yang sama dapat kita gunakan untuk menentukan luas daerah yang terletak di bawah sumbu-

x

. Misalkan terdapat daerah

B

dengan kurva pembatas area:

y = f (x), x = a, x = b

, dan sumbu-

x

, dengan

f (x) \leq 0

. Pengintegralan fungsi

f (x)

pada interval

a \leq x \leq b

akan bernilai negatif. Oleh karena luas selalu bernilai positif, maka luas daerah yang dibatasi kurva

f (x) \leq 0

pada interval

a \leq x \leq b

tersebut adalah

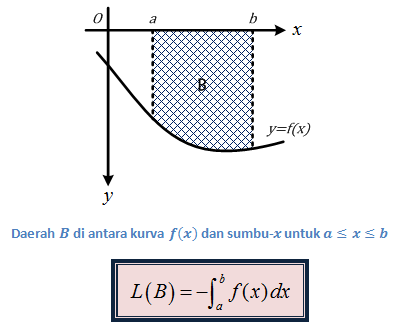
Oleh karena terdapat dua rumus berbeda, maka perlu diperhatikan apakah fungsi tersebut berada di atas atau di bawah sumbu-

x

. Ada beberapa fungsi yang diketahui sudah pasti selalu di atas sumbu-

x

. Beberapa fungsi yang nilainya selalu positif, antara lain:

f (x) = x^{2} \geq 0

,dengan

x \in R

;

f (x) = x^{2 n}

, dengan

x \in R

dan

n \in N

;

\cos x

, dengan

- \frac{π}{2} \leq x \leq \frac{π}{2}

;

dan

\sin x

, dengan

0 \leq x \leq π

Sementara untuk fungsi yang belum jelas diketahui posisinya terhadap sumbu-

x

, harus digambarkan terlebih dahulu untuk memutuskan rumus yang digunakan.

Berikut ini beberapa contoh gambar fungsi secara umum.

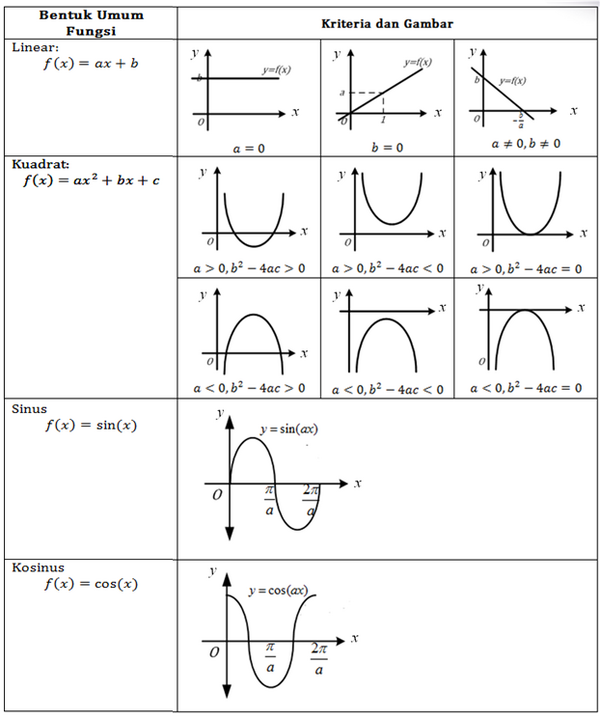
Untuk lebih memahami kedua kasus ini, maka perhatikan contoh berikut.

☘ Contoh Soal 1

Luas daerah yang dibatasi oleh kurva

f (x) = 1 + x^{2}, x = 1, x = 4

, dan sumbu–

x

adalah ….

✎ Penyelesaian

Perhatikan bahwa

x^{2} \geq 0

untuk setiap

x \in R

sehingga

1 + x^{2} \geq 0

. Ini berarti, daerah tersebut terletak di atas sumbu-

x

.

Pada grafik, terlihat bahwa kurva berada di atas sumbu–

x

pada selang

1 \leq x \leq 4

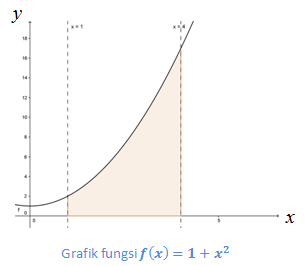
Dengan demikian, luas daerah tersebut adalah:

\begin{aligned} L = \int_{1}^{4} f (x) d x & = \int_{1}^{4} 1 + x^{2} d x \\ = {| x + \frac{1}{3} x^{3} |}_{1}^{4} \\ = 4 + \frac{1}{3} {.4}^{3} - (1 + \frac{1}{3} {.1}^{3}) \\ = 3 + \frac{63}{3} \\ = 24 \end{aligned}

Dengan demikian, luas daerah yang dibatasi oleh kurva

y = 1 + x^{2}, x = 1, x = 4

, dan sumbu–

x

adalah 24 satuan luas.

☘ Contoh Soal 2

Luas daerah yang dibatasi oleh kurva

f (x) = \cos x, x = \frac{π}{2}, x = π

, dan sumbu–

x

adalah ….

✎ Penyelesaian

Perhatikan bahwa batasan pengintegralan

\frac{π}{2} \leq x \leq π

merupakan daerah kuadran II dan pada kuadran kedua

\cos x

bernilai negatif, sehingga

f (x) \leq 0

.

Dengan demikian, luas daerah tersebut adalah:

\begin{aligned} L & = - \int_{\frac{π}{2}}^{π} \cos x d x \\ = - (\sin x |_{\frac{π}{2}}^{π}) \\ = - (0 - 1) \\ = 1 \end{aligned}

Dengan demikian Luas daerah yang dibatasi oleh kurva

f (x) = \cos x, x = \frac{π}{2}, x = π

, dan sumbu–

x

adalah 1 satuan luas.

Kurva Memotong Sumbu-x

Selanjutnya akan dibahas luas daerah yang dibatasi sumbu–

x

dan memotong sumbu–

x

. Misalkan

f (x)

adalah fungsi kontinu pada selang

a \leq x \leq b

dan

f (x)

memotong sumbu–

x

di titik

x = c

, dengan

f (x) \geq 0

untuk selang

a \leq x \leq c

dan

f (x) \leq 0

untuk selang

c \leq x \leq b

. Luas daerah yang dibatasi oleh

f (x)

dan sumbu–

x

pada selang

a \leq x \leq b

adalah:

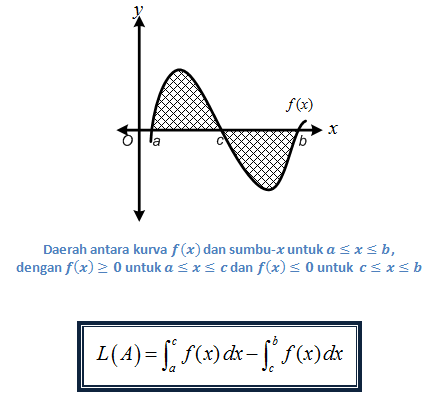
☘ Contoh Soal 3

Luas dari daerah yang dibatasi oleh kurva

y = 4 x^{3}, x = - 3

, dan

x = 4

serta sumbu–

x

adalah ….

✎ Penyelesaian

Perhatikan bahwa,

4 x^{3}

bernilai negatif jika

x

negatif dan bernilai positif jika

x

positif, sehingga

f (x) \geq 0

untuk selang

- 3 \leq x \leq 0

dan

f (x) \geq 0

untuk selang

0 \leq x \leq 4

.

Dengan demikian, luas daerah tersebut adalah:

\begin{aligned} - \int_{- 3}^{0} 4 x^{3} d x + \int_{0}^{4} 4 x^{3} d x & = - (x^{4} |_{- 3}^{0}) + x^{4} |_{0}^{4} \\ = - (0^{4} - (- 3)^{4}) + 4^{4} - 0^{4} \\ = 81 + 256 \\ = 337 \end{aligned}

Jadi, luas daerah tersebut adalah 337 satuan luas.

☘ Contoh Soal 4

Luas daerah yang dibatasi kurva

y = x + \sin x, x = - π, x = π

, dan sumbu–

x

adalah ….

✎ Penyelesaian

Perhatikan bahwa,

y \leq 0

pada selang

- π \leq x \leq 0

dan

y \geq 0

pada selang

0 \leq x \leq π

.

Dengan demikian, daerah tersebut harus dibagi (dipartisi) menjadi dua bagian yaitu untuk selang

- π \leq x \leq 0

dan

0 \leq x \leq π

.

Luas daerah tersebut adalah:

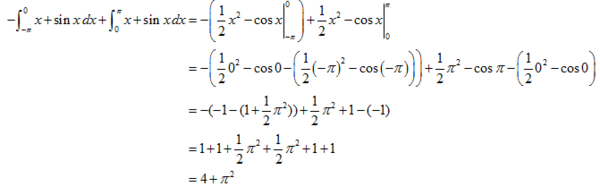
Jadi, luas daerah yang dibatasi kurva

y = x + \sin x, x = - π, x = π

, dan sumbu-

x

adalah

4 + π^{2}

satuan luas.

Cara lain menentukan partisi dari daerah tersebut adalah dengan melihat grafiknya, sebagai berikut.

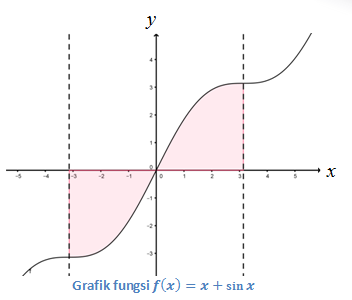
☘ Contoh Soal 5

Luas daerah yang diarsir pada gambar berikut adalah ….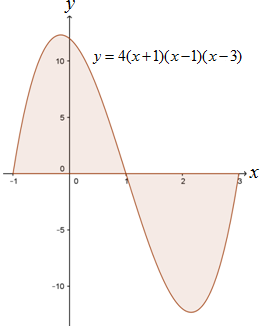

✎ Penyelesaian

Perhatikan bahwa kurva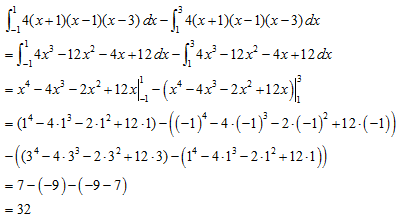

y = 4 (x + 1) (x - 1) (x - 3)

berada di atas sumbu-

x

untuk

- 1 \leq x \leq 1

dan berada di bawah sumbu-

x

untuk

1 \leq x \leq 3

, sehingga luas daerah tersebut adalah:

Jadi, luas daerah tersebut adalah 32 satuan luas.

KESIMPULAN

Sumber : Quipper school

Nah, kalian telah selesai belajar tentang luas daerah yang dibatasi oleh sumbu-y. Agar pemahaman kalian bertambah lagi, yuk kerjakan latihan soal-soal berikut ini.

Soal Latihan dan Pembahasan

Pembahasan Cara Smart

Video Pembahasan

Integral - Luas Daerah Yang Dibatasi Kurva dan Sumbu x

Kurva Tidak Memotong Sumbu- $x$

1. Daerah terletak di atas sumbu- $x$