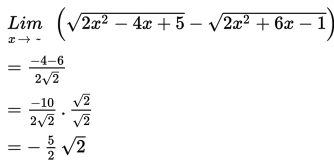Pada topik ini kalian akan belajar tentang 2 materi sekaligus, yaitu limit fungsi trigonometri dan limit fungsi aljabar untuk x -> ~
Limit Trigonometri
Untuk mempelajari limit fungsi trigonometri, tentunya kalian harus ingat rumus-rumus trigonometri yang nantinya akan sering digunakan.
Mari kita ingat kembali rumus-rumus trigonometri berikut :
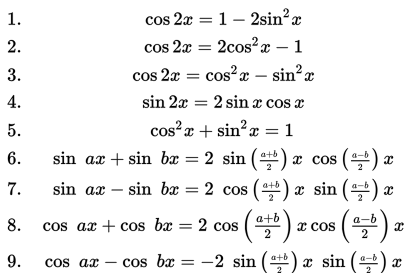
Pengertian
Limit fungsi trigonometri adalah limit yang memuat perbandingan trigonometri.
Bentuk umum penulisan
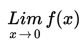
dengan f(x) adalah fungsi yang memuat perbandingan trigonometri
Rumus-rumus limit fungsi trigonometri
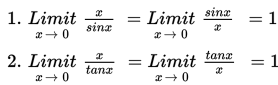
Untuk cosinus tidak berlaku seperti rumus di atas
Contoh 1
Hitung nilai dari
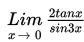
Penyelesaian :
Jika kita substitusikan nilai x = 0, maka diperoleh :
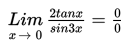
Agar tidak diperoleh bentuk 0/0, maka untuk menyelesaikannya kita gunakan rumus trigonometri sebagai berikut :

Contoh 2
Hitung nilai
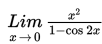
Penyelesaian :
Jika kita substitusikan x = 0, maka diperoleh :
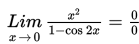
agar tidak diperoleh bentuk 0/0, maka digunakan rumus cos 2x = 1 – 2 sin2 x
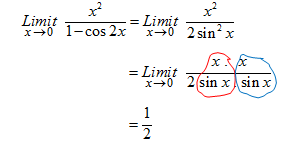
Contoh 3
Hitung nilai
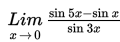
Penyelesaian :
Jika kita substitusikan x = 0, maka diperoleh :
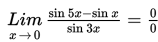
agar tidak diperoleh bentuk 0/0, maka digunakan rumus
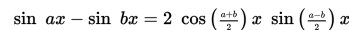
sehingga diperoleh :

Limit Fungsi Aljabar untuk x -> ~
Pengertian
Limit fungsi aljabar untuk x -> ~ adalah limit dengan nilai x mendekati tak hingga.
Mari kita perhatikan tabel berikut :
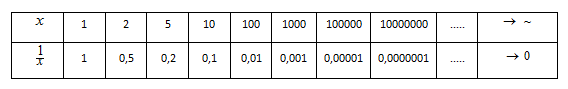
Dari tabel di atas, terlihat bahwa untuk nilai x mendekati tak hingga diperoleh nilai 1/x mendekati 0.
Dengan demikian,
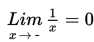
Cara menyelesaikan limit fungsi aljabar untuk x -> ~
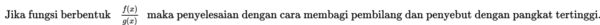
Jika fungsi berbentuk f(x) ± g(x) dengan f(x) dan g(x) masing-masing fungsi irasional (bentuk akar), maka penyelesaian dengan cara mengalikan dengan sekawan dari bentuk f(x) ± g(x), kemudian dilanjutkan dengan cara seperti no. 1 di atas.
Contoh 4
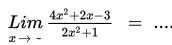
Penyelesaian :
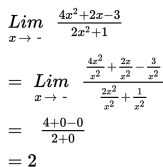
Contoh 5
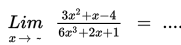
Penyelesaian :
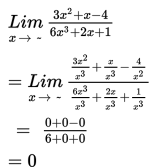
Contoh 6
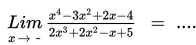
Penyelesaian :
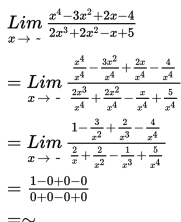
Contoh 7
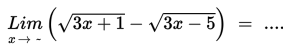
Penyelesaian :

Contoh 8
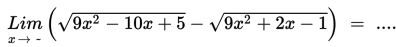
Penyelesaian :

Dari beberapa contoh di atas, dapat kita simpulkan bahwa langkah-langkah menghitung nilai limit untuk x -> ~ dapat disesuaikan dengan bentuk fungsi limitnya :
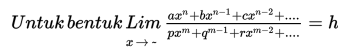
1. Jika n = m, maka nilai h = a/p
2. Jika n < m, maka nilai h = 0
3. Jika n > m, maka nilai h = ~
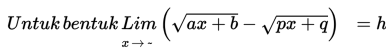
1. Jika a = p, maka nilai h = 0
2. Jika a < p, maka nilai h = - ~
3. Jika a > p, maka nilai h = ~
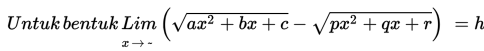
a. Jika a = p, maka nilai h = (b - q) / 2√a
b. Jika a < p, maka nilai h = - ~
c. Jika a > p, maka nilai h = ~
Contoh 9
Hitung nilai
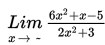
Penyelesaian :
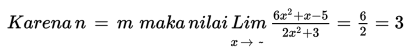
Contoh 10
Hitung nilai
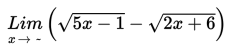
Penyelesaian :
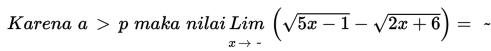
Contoh 11
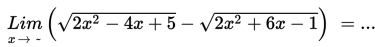
Penyelesaian :
Karena a = p maka