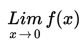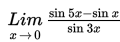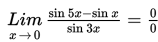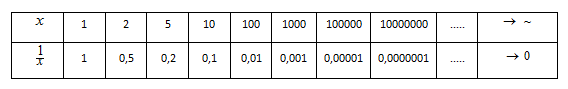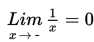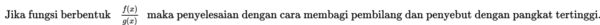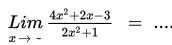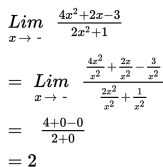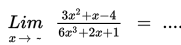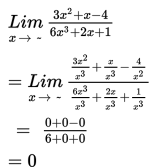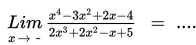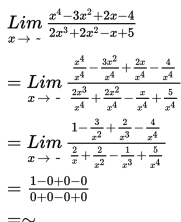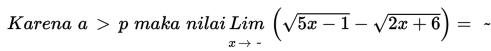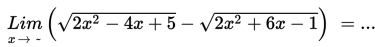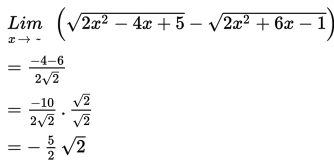Pada topik sebelumnya, kalian telah belajar mengenal konsep limit fungsi, sedangkan dalam topik ini kalian akan belajar tentang penerapan konsep limit dalam konteks nyata.
Mari kita ingat kembali konsep limit fungsi.
Pengertian Limit
Limit berarti pendekatan. Limit fungsi f(x) untuk x mendekati c sama artinya dengan pendekatan nilai f(x) untuk x = c. Selanjutnya, limit fungsi ini ditulis seperti berikut :
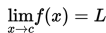
Secara intuitif, jika f : R → R , L dan c merupakan bilangan real, maka berlaku hubungan sebagai berikut :
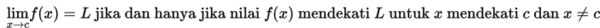
Apakah kalian masih ingat dengan limit kanan dan limit kiri?
Limit Kanan

Limit Kiri
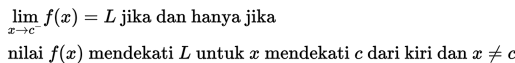
Jika diberikan fungsi f : R → R dengan L dan c bilangan real, maka berlaku pula konsep limit kanan dan limit kiri berikut ini :
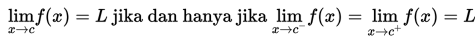
Selanjutnya, untuk menyelesaikan limit fungsi aljabar, digunakan metode berikut :
- substitusi langsung
- faktorisasi
- menyederhanakan
Limit Fungsi di tak hingga
Limit fungsi f(x) untuk x mendekati tak hingga ditulis seperti berikut :
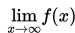
Seperti yang telah kalian ketahui, dalam limit fungsi di tak hingga, berlaku hubungan sebagai berikut :

Adapun cara untuk menyelesaikan limit fungsi di tak hingga adalah sebagai berikut :
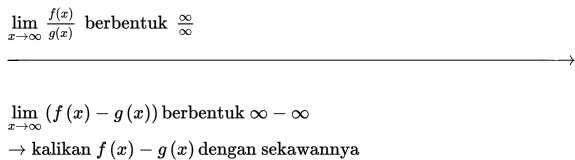
Sifat - Sifat Limit
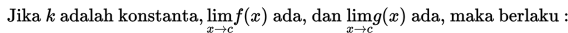

Konsep limit dalam konteks nyata diantaranya dapat dijumpai dalam bidang fisika dan ekonomi.
Penerapan limit dalam bidang fisika
Kecepatan sesaat adalah limit dari kecepatan ata-rata dan dapat dinyatakan seperti berikut ini :
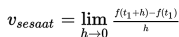
Percepatan gerak benda adalah limit dari percepatan rata-rata dan dinyatakan seperti berikut
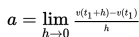
Penerapan limit dalam bidang ekonomi
Konsep limit dalam bidang ekonomi sering digunakan untuk menentukan biaya marjinal (marginal cost) dan penerimaan marjinal (marginal revenue).
Biaya marjinal adalah laju perubahan sesaat biaya terhadap banyaknya barang yang dihasilkan, sedangkan penerimaan marjinal adalah laju perubahan sesaat penerimaan terhadap banyaknya barang yang dihasilkan.
Biaya marjinal dan penerimaan marjinal dinyatakan sebagai berikut :
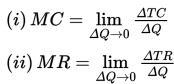
Mari kita cermati contoh berikut ini.
Contoh :
Seutas tali dengan panjang satu satuan panjang, dipotong menjadi 2 bagian yang sama, lalu ½ bagian dari tali itu dibagi 2 lagi, kemudian ¼ bagian dari tali itu dipotong menjadi 2 lagi, dan seterusnya. Apa yang dapat kamu simpulkan?
Penyelesaian :

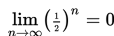
Jika tali tersebut dipotong terus menerus, dengan panjang potongan berikutnya adalah setengah kali potongan semula, maka berdasarkan nilai limit di atas, tali tersebut pada akhirnya akan habis dan tidak lagi dapat dipotong.